mZK equation
Background
Copiado de 1:
The Zakharov-Kuznetsov (ZK) equation is a mathematical model used to study the behavior of weakly nonlinear ion-acoustic waves in the presence of a uniform magnetic field. The equation describes the interaction between hot isothermal electrons and cold ions and can also be applied in the analysis of the generalized stationary Gardner equation.
Copiado de Este:
Kuznetsov together with Zakharov [10] presented the equation
$$ u_t+u u_x+\nabla^2 u_x=0 \tag{2} $$which recounts the progression of the infirmly nonlinear ion with acoustic waves within a plasma comprising hot plutonic electrons alongside cold ions in the attendance of an unvarying magnetic field pushed in the direction of -axis. Eq. (2) also emerged in sundry other fields in science counting, optical fibre, geochemistry, as well as physics in solid states [11], [12], [13], [14]. This type of equation is found out to govern diverse as well as varieties of physical phenomena, in the purely dispersive limit, thus including the Rossby waves in a rotating atmosphere [15], long waves subsisting on a thin liquid film [16], as well as the isolated vortex of drift waves in a plasma that is three-dimensional [17]. Shivamoggi in Shivamoggi [18] dispensed a detailed discourse which brought to play the analytical features of (2). Besides, Nawaz et al. [19] instituted pertinent solutions to the ZK equations which possess full nonlinear dispersion property via the homotopy analysis approach.
Papers que he encontrado
Maple 085.
Otra paper que habla de la misma es este. Pero no es exactamente la misma eq.
En este otro paper sale una parecida, pero no igual.
En este otro parece que nos acercamos un poco más, porque sale término de segundo grado.
Aquí ya por fin sale la misma, pero con coeficientes variables. Buena revista. Este también y con coeficientes constantes!! También con coeficientes constantes en este.
Encuentro cinf-structure siguiendo la determining equation, y la uso para encontrar dos familias uniparamétricas ($C_3=C_2=0$) de travelling waves.
Por una parte, usando la $I_1$ que he llamado "I1modifsimple" en el fichero maple. Incluyen al caso 1. Dependen de todos los parámetros de la ecuación, de la $c$ y de $C_1$, luego respecto de la PDE constituyen una familia biparamétrica:
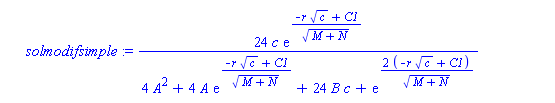
En la nueva nomenclatura es sol4 (con C1/sqrt(c)). Es la misma que sol 1 con otra C1.
Con Lie, forzando a Maple a hacer la integral y a simplificar, se llega a lo mismo
Por otra parte, usando la $I_1$ que he llamado "I1simple" obtengo "solsimple", que tras eliminar el número imaginario obtengo "soluc":
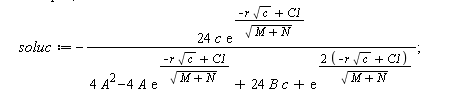
En la nueva nomenclatura es sol2 o sol2correg (con C1/sqrt(c)).
Puede que solmodifsimple y soluc sean la misma familia, pero tomando valores complejos para $C_1$.
Las soluciones del paper
Caso 1
Si en mi familia solmodifsimple tomamos $c=- \lambda (M+N)$ y
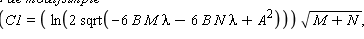
entonces sale el caso 1 del paper.
Caso 2
Asumimos, como ellos $B(M+N)<0$.
Si en mi familia solsimple tomamos $c=-\frac{A^2}{6B}$ y

sale el caso 2 de ellos.
Caso 3
Fijando $c=-\frac{3 A^2}{16 B}$ de antemano, podemos llegar a una familia de soluciones que solamente es válida para este valor de $c$. Es independiente de las otras familia, pues aparece con $C_3=-\frac{9 A^4}{1024 B^3 (M+N)}$. La familia es
$F=$
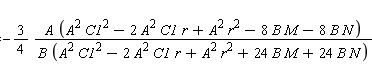
Tomando $C_1=0$ sale el caso 3 de ellos
Otra familia no invertible
Encuentro otra familia uniparamétrica, despejando $v_1$ en vez de $v_2$ en la $I_3$, pero no sé invertirla (es decir, encuentro $r(v)$). A esto creo que no se llega con Lie
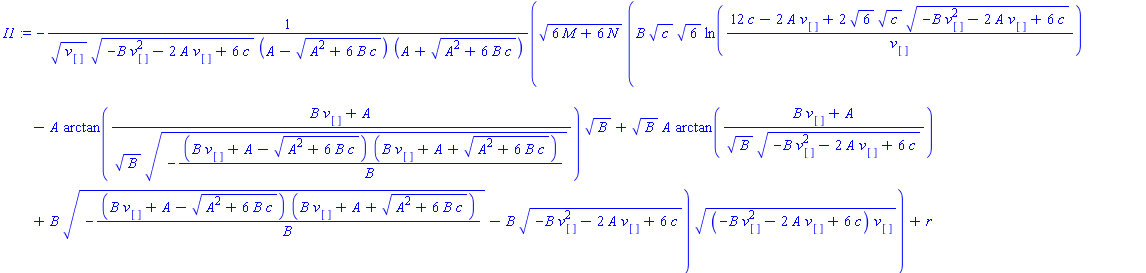
Expresión general de las travelling wave
La solución general (su inversa) se puede expresar con las raíces de un polinomio de grado 4. A esto se llegaría también usando Lie...

El polinomio es el que aparece dentro de la raíz cuadrada en el denominador
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: